Field of View Explained - What Is FOV & How Does It Relate To Binoculars & Scopes?

Is field of view important when choosing a binocular or rifle scope?

Does it have any relation to eye relief and magnification?

We'll go over field of view and the tidbits you need to know without requiring an engineering degree to understand it.

Let's get into the overview of the field ahead!

What is Field of View?

Field of view (FOV) is the measured area of the scene you can see when looking through your optic.  It is determined by multiple components in the optic that includes the eyepiece, thickness of the lenses, position in its assembly, and magnification.

As there are many structural and design elements that govern FOV, we'll just leave that to the manufacturer, but we can master the numbers, so we know what we're getting or what we're missing out on when buying a sport optic.

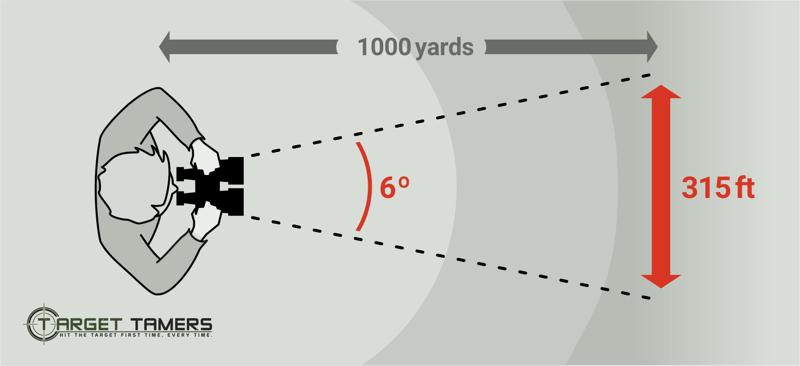
How is Field of View Measured?

FOV is provided by manufacturers in multiple measurements.  Binoculars, rangefinders, and spotting scopes tend to measure FOV in feet at 1000 yards.  Rifle scopes provide FOV in feet at 100 yards.

If a binocular says it has FOV of 341 feet at 1000 yards, it means you can see 341 feet of a scene from left to right when looking at 1000 yards.  Measurements in feet, meters, and yards are called the linear field of view.

Sometimes, you'll see FOV provided in angular degrees.  A rangefinder may have an angular FOV of 6.0°.  The higher the angle, the wider the field of view, and the angular FOV remains the same at any given distance.  To calculate angular to linear FOV is easy.  Multiply the angle by 52.5 to get the linear feet FOV.

For example, the rangefinder with 6.0° FOV x 52.5 equals 315 feet at 1000 yards.  This is because one angle degree is equal to 52.5 feet.

Magnification, Eye Relief, and Field of View

Yes, almost every feature on an optic has to do with the mechanisms of another feature.  So, how does magnification affect field of view?

The rule is simple.  Increase magnification, decrease field of view.  When you crank up the power on your scope, you're going to see less of an area as you get more specific detail on your target or scene.

When you dial back down to low magnification, the field of view will become wider as you see more of the surroundings in your view. Notice the change in field of view looking through my scope at 5x compared to 15x magnification:

Where does eye relief come in?

If you're too close or too far outside of the given eye relief distance, your view of the surroundings through your optic is going to be affected.  You may see the Field Of View (FOV) slightly blocked out or part of the FOV is "clipped."  This is called vignetting.

Sometimes being too far out of the given eye relief distance might cause a shadowing or ring of vignetting around the entire edge of the FOV.  You will want to get your eyes within the eye box (within given eye relief specs) to ensure you have a clear and unobstructed Field Of View (FOV).

What is Tunneling?

Tunneling is usually noticed and experienced with rifle scopes, although other zoom/variable power optics can have this malfunction.  Tunneling is when the field of view does not increase or decrease when you change magnification.

While some scopes tend to have this issue at lower magnifications, it can happen across the entire magnification range, and some power levels may be worse than others.

For example, on a 5-20x rifle scope, the Field Of View (FOV) should be larger at 5x than it would be at 7x.  When you increase magnification, you lose FOV.  When you lower magnification, you increase field of view.  However, when experiencing tunneling, the FOV would stay exactly the same at 7x as it is at 5x.

There was no gain or increase in FOV when dialing down in power from 7-5x.  This indicates that neither the magnification or FOV are directly proportional in this case.  The scope is no longer a true 5-20x scope, it's now a 7-20x scope.

Check out an example of this in the video below:

Why does this happen?

Some manufacturers take short cuts to promote a product that's technically been pushed out of its optical limits.

Other times, additional components have been added to an optics assembly to compensate for lens and coating defects and to minimize chromatic aberration and lens distortion.  However, these additional components in the optical path can cause tunneling.

Can you be sure what scopes have tunneling issues before you buy?  No manufacturer I'm aware of advertises tunneling as a feature, benefit, or advantage.

The buying process is a perfect example of doing some purposeful digging and research before you buy.  Reading the rifle scope reviews, checking in with the masses, and doing your homework will go a long way.

An Overview of the Field of View

We promised to give you the plain view of the field of view without any fancy fluff.  There you have it.  It was easy enough, right?

Knowing the Field Of View (FOV) may be important for what you want to do.  If it's birdwatching, a wide field of view will make it easier to track moving birds.  If it's sub-500-yard hunting, standard rifle scope FOVs will work just fine.

Just remember to get your eye in line with the eye box and don't be afraid to use magnification as you need it.

Further Reading

• 10 Good Reasons to Start Using a Hunting Rangefinder Today
• How To Use A Rangefinder To Improve Your Target Shooting Skills
• 5 Tips to Maximize Rangefinder Efficiency in Any Light or Weather
• Glossary of Hunting Rangefinder Terms & Features (Made Easy)
• The Best Angle Compensating Rangefinders & Beginners Guide